Be cautious when there’s some, be cautious when there’s none, and be cautious when adding more than one.
What do the heck does that mean???
Let’s take these correlation cautions one by one.
Be cautious when there’s some. Suppose you did a study and found a correlation between job performance and high school grades. Does this mean that if we simply increase everyone’s high school grades that they will perform better at work??? Clearly not!
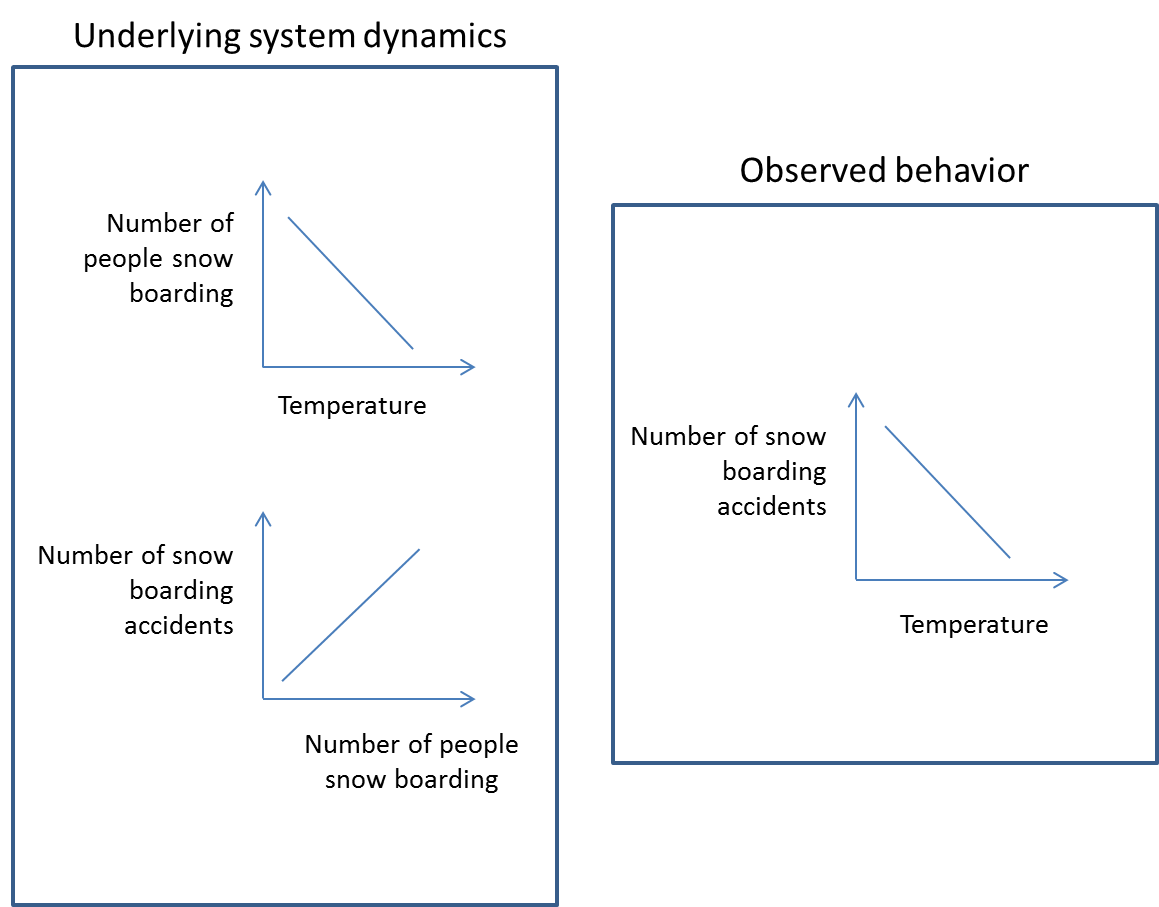
Just because two variables are correlated, it does not necessarily mean that one causes the other. It could be an accidental correlation or it could be the indication of a relationship caused by lurking variables or systems. So, if a researcher were to establish a negative correlation between the air temperature and the number of snow boarding accidents, my bet is that the cold air isn’t responsible, but there is a lurking variable, namely more people snow board when it is cold!
Be cautious when there’s none. So you are punching data into a statistical package of one kind or another and you find that there is little to no correlation between an input and an output. That means the input doesn’t cause the output, right??? ABSOLUTELY NOT!
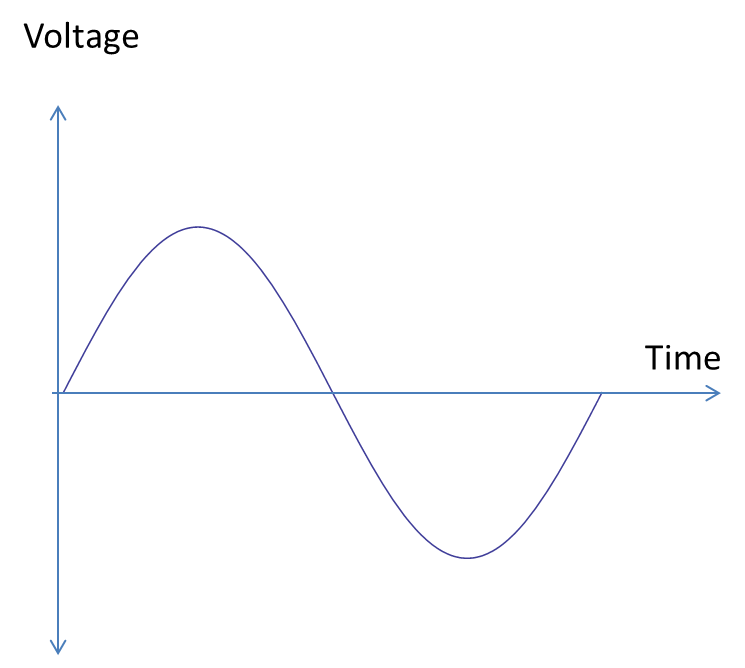
If there is a correlation between an input and an output it means that there is a linear relationship between them. Just because there isn’t a linear relationship, it doesn’t mean that there isn’t a relationship. There are many things that have a non-linear relationship such as: the voltage as a function of time relationship for an AC circuit; the relationship between how much kinetic energy a car has and its velocity; or the intensity of a light bulb as a function of distance.
Be cautious when adding more than one. This is known as Simpson’s paradox (no, not Homer Simpson!). Suppose you have a set of data that shows a positive correlation between variable x and variable y. And further suppose you have a second or third dataset that also shows the same positive correlation between variable x and variable y. When you combine all the datasets you can actually end up with a negative correlation between x and y! That is the paradox.
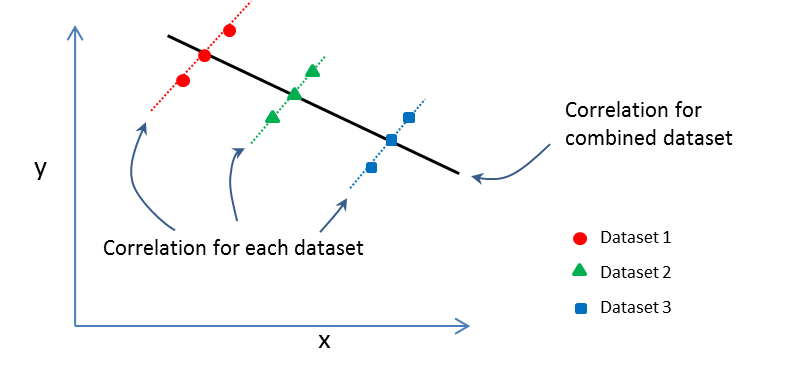How could this ever happen? Well, one way would be if you combined data from three measurement systems that were uncalibrated.
So the moral of the story is this:
- Correlation does not mean causation.
- Lack of a correlation does not mean lack of a relationship.
- Combining datasets can have a paradoxical result on correlations.
