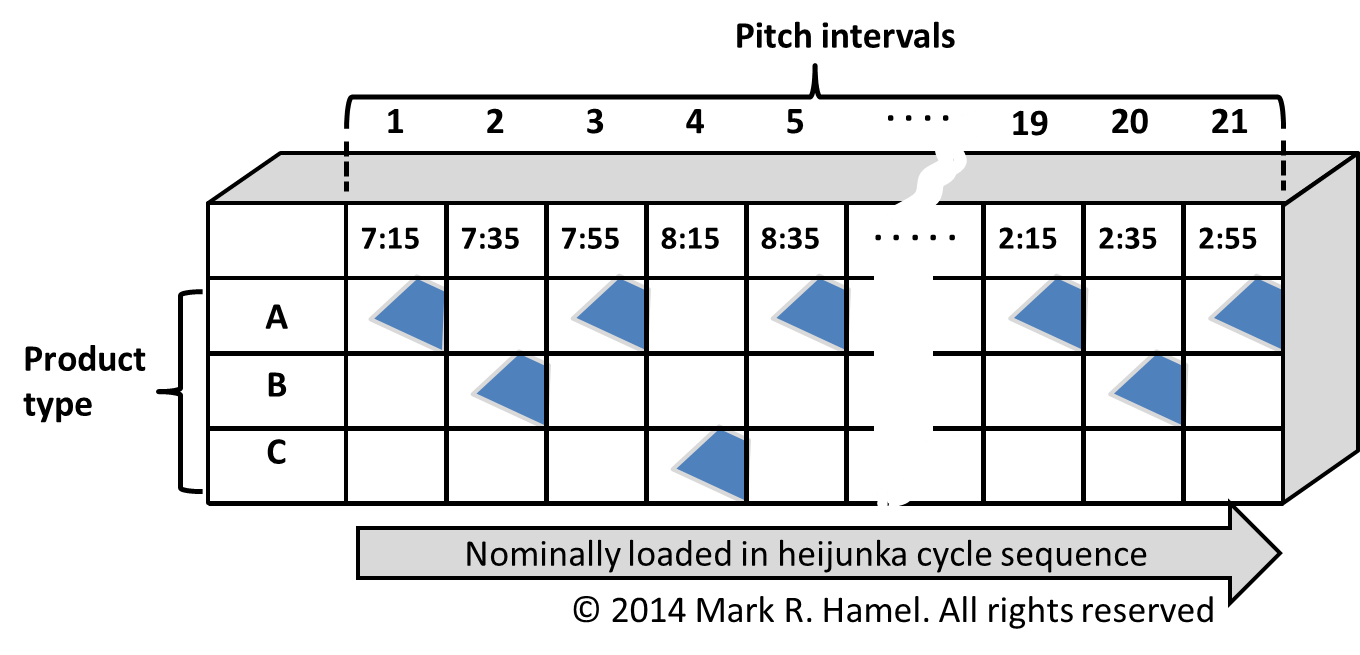
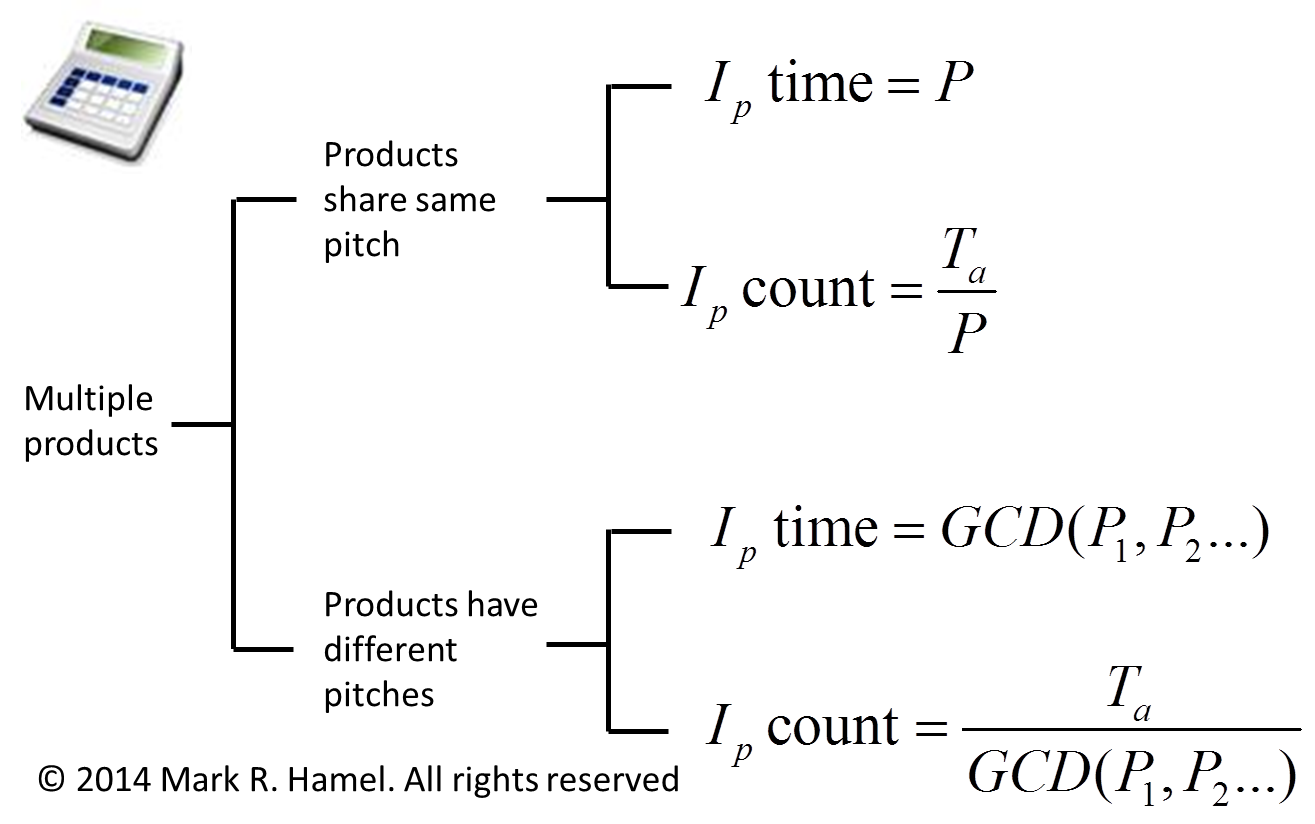Pitch interval (Ip) can be thought of in two ways: 1) as a unit of time representing the (usually) smallest common pitch shared among a range of products, services, or transactions that are being produced, conveyed, performed, or executed by a given resource(s), and 2) as a count of the number of intervals of a common pitch over a period of time, typically a shift or day. Ip often serves as the time intervals reflected in the typical design of heijunka, leveling, or scheduling boxes or boards in which instruction or withdrawal kanban are loaded within the heijunka sequence (as accommodated by actual demand). Figure 1 captures the Ip math. This post is specific to products that share the same pitch. A future post will address Ip for products that have different pitches. Figure 2 provides some insight into heijunka box design and loading in the context of Ip.
Figure 1. Pitch interval formula tree
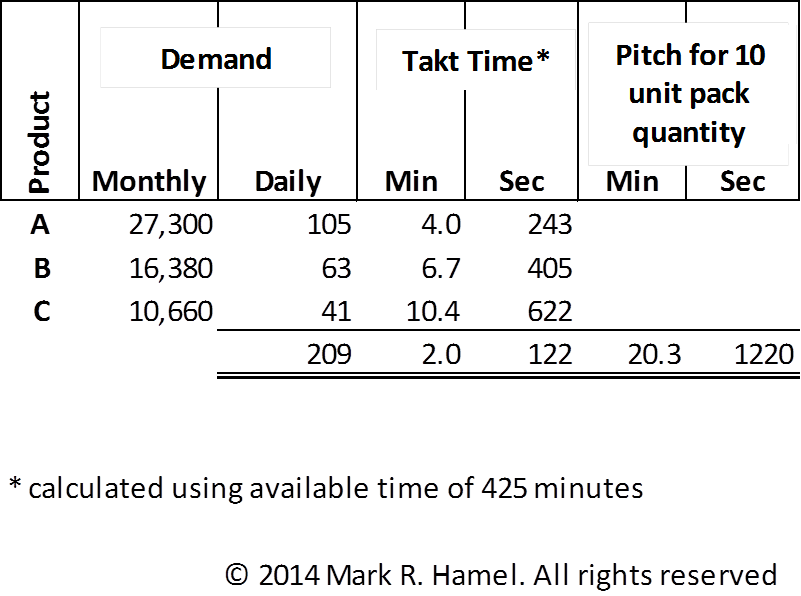
Where: Ta = available time for the period, typically a shift or day and expressed in seconds or minutes P = pitch for the resource(s) related to Ta and expressed in the same unit of time. GCD notation represents the greatest common divisor, also known as greatest common factor or highest common factor, for a given set (a, b…) Pn = each non-equal pitch amongst the various products for the resource(s) related to Ta and expressed in the same unit of time. Same Pitch Example: There are three products (A, B, and C), all of which share the same 20 minute pitch. See table below for the pitch calculation.
Table 1. Pitch calculation
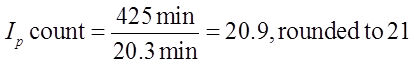See Figure 2 for example heijunka box as loaded in an ABACABACAB sequence (a.k.a. heijunka cycle).
Figure 2. Heijunka box reflecting 20 minute intervals.
Remember, life is messy…and sometimes the math is too. The lean practitioner often needs to use his or her judgment when determining whether or not to round and how to round (up or down). Unfortunately, math rarely comes out perfect (as it magically does in most lean books). When addressing things like pitch intervals, know that rounding has practical implications. For example, rounding up the number of pitch intervals may require either the shortening of the pitch (remember Ip x P should closely approximate Ta) equally across all or some intervals. In the example above, by rounding up to 21 intervals, we are artificially speeding up takt time by two seconds per unit, and thus our pitch by 20 seconds. The cumulative effect is that the last pitch interval of the day actually finishes up 5 minutes early. The lean practitioner has some options here: 1) don’t sweat it and do nothing about the 5 minutes early thing, 2) use a 21 minute pitch after every third interval, or 3) tinker with something else. As you may discern from Figure 2, we think option one is fine. Know that the road to figuring out the best option often requires a good bit of PDCA. Related posts: Available Time, Heijunka Cycle
