Let’s suppose there are three BIG potential orders in your sales pipeline. What are your chances that you are going to win an order? This is a question that faces manufacturing and service industries all the time. If they chase too much business, they run the risk of winning the business and not being able to fulfill the request but if they don’t chase any business, they run the risk of being idle. To illustrate the math behind this important question let’s suppose the following: 
So what are your chances of winning an order? Clearly, it isn’t the sum of the probabilities of success. You can’t have a 110% chance of winning an order. And clearly the chance of success has to be greater than 50% because it has to be at least as large as you highest chance of winning. This is one of those interesting math questions that comes up frequently and fortunately has a simple solution. The trick is to not calculate the probability of winning an order, but instead to calculate the probability of not winning any orders and then take it from there. This is because if you know the probability of not winning any orders, then the probability of winning an order must be one minus that probability. If we assume that the orders are independent, the probability of not winning any orders is: 
So therefore, there is a 76% chance of winning at least one order. Another way to solve this problem would have been to enumerate all the possible outcomes and then count how many times each outcome occurs and divide that number by the total number of outcomes to determine the probability for that outcome to occur (see Figure 1).
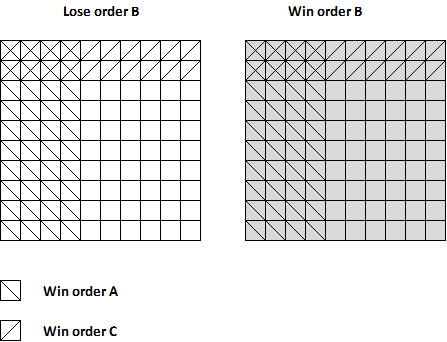Figure 1: Illustration of all of the possible outcomes for orders A, B, and C. There are 200 cells shown, each cell represents one possible outcome. Half of the cells are shaded, representing the 50% chance of winning order B. 40% of the cells have a upper left to bottom right diagonal (representing the probability of winning of order A), and 20% of the cells have a bottom left to upper right diagonal representing those outcomes where order C is won. Cells with no shading or diagonals are those cases where no orders are won. There are 48 cases where that happens. Since there are 200 possible outcomes, the chance of winning no orders is 48/200 or 24%.
For cases where enumerating all the possible outcomes are difficult, one might rely on the basic rules of probability such as:
- The probability of an event happening is, one minus the probability of it not happening (i.e. Subtraction rule)
- The probability of several independent events happening is the product of the probability of the events happening (i.e. Special multiplication rule)
- The total probability for mutually exclusive events to occur is the sum of their probabilities (i.e. Addition rule)
For more rules of basic probability, see: The Cartoon Guide to Statistics, by Larry Gonick and Woollcott Smith.
